দৈনন্দিন জীবনে আমাদের চারপাশে যা কিছু দেখি ও ব্যবহার করি এর কিছু চারকোনা, কিছু গোলাকার। আমাদের ঘরবাড়ি, দালানকোঠা, দরজা-জানালা, খাট-আলমারি, টেবিল-চেয়ার, বই-খাতা ইত্যাদি সবই চারকোনা। এদের ধারগুলো সরলরেখা হিসেবে বিবেচনা করলে দেখা যায় যে, এরা সমদূরবর্তী বা সমান্তরাল।
সমান্তরাল সরলরেখা ও ছেদক দ্বারা উৎপন্ন কোণের বৈশিষ্ট্য ব্যাখ্যা করতে পারবে।
দুটি সরলরেখা সমান্তরাল হওয়ার শর্ত বর্ণনা করতে পারবে।
দুটি সরলরেখা সমান্তরাল হওয়ার শর্ত প্রমাণ করতে পারবে।
প্রতিজ্ঞা: জ্যামিতিতে যে সকল বিষয়ের আলোচনা করা হয়, সাধারণভাবে তাদের প্রতিজ্ঞা বলা হয়।
সম্পাদ্য: যে প্রতিজ্ঞায় কোনো জ্যামিতিক বিষয় অঙ্কন করে দেখানো হয় এবং যুক্তি দ্বারা অঙ্কনের নির্ভুলতা প্রমাণ করা যায়, একে সম্পাদ্য বলা হয়।
সম্পাদ্যের বিভিন্ন অংশ:
(ক) উপাত্ত: সম্পাদ্যে যা দেওয়া থাকে, তাই উপাত্ত।
(খ) অঙ্কন: সম্পাদ্যে যা করণীয়, তাই অঙ্কন।
(গ) প্রমাণ: যুক্তি দ্বারা অঙ্কনের নির্ভুলতা যাচাই হলো প্রমাণ।
উপপাদ্য: যে প্রতিজ্ঞায় কোনো জ্যামিতিক বিষয়কে যুক্তি দ্বারা প্রতিষ্ঠিত করা হয়, একে উপপাদ্য বলে।
উপপাদ্যের বিভিন্ন অংশ:
(ক) সাধারণ নির্বচন: এ অংশে প্রতিজ্ঞার বিষয়টি সরলভাবে বর্ণনা করা হয়।
(খ) বিশেষ নির্বচন: এ অংশে প্রতিজ্ঞার বিষয়টি চিত্র দ্বারা বিশেষভাবে দেখানো হয়।
(গ) অঙ্কন: এ অংশে প্রতিজ্ঞা সমাধানের বা প্রমাণের জন্য অতিরিক্ত অঙ্কন করতে হয়।
(ঘ) প্রমাণ: এ অংশে স্বতঃসিদ্ধগুলো এবং পূর্বে গঠিত জ্যামিতিক সত্য ব্যবহার করে উপযুক্ত যুক্তি দ্বারা প্রস্তাবিত বিষয়টিকে প্রতিষ্ঠিত করা হয়।
অনুসিদ্ধান্ত: কোনো জ্যামিতিক প্রতিজ্ঞা প্রতিষ্ঠিত করে এর সিদ্ধান্ত থেকে এক বা একাধিক যে নতুন সিদ্ধান্ত গ্রহণ করা যায়, এদেরকে অনুসিদ্ধান্ত বলা হয়।
আধুনিক যুক্তিমূলক জ্যামিতির আলোচনার জন্য কিছু মৌলিক স্বীকার্য, সংজ্ঞা ও চিহ্নের প্রয়োজন হয়।
কোনো সরলরেখা দুই বা ততোধিক সরলরেখাকে বিভিন্ন বিন্দুতে ছেদ করলে একে ছেদক বলে।
চিত্রে, AB ও CD দুটি সরলরেখা এবং LM সরলরেখাগুলোকে যথাক্রমে দুটি ভিন্ন বিন্দু P,Q তে ছেদ করেছে। LM সরলরেখা AB ও CD সরলরেখাদ্বয়ের ছেদক। ছেদকটি AB ও CD সরলরেখা দুইটির সাথে মোট আটটি কোণ তৈরি করেছে। কোণগুলোকে ∠1,∠2,∠3,∠4,∠5,∠6,∠7,∠8 দ্বারা নির্দেশ করি। কোণগুলোকে অন্তঃস্থ ও বহিঃস্থ, অনুরূপ ও একান্তর এই চার শ্রেণিতে ভাগ করা যায়।
| অন্তঃস্থ কোণ | ∠3,∠4,∠5,∠6 |
| বহিঃস্থ কোণ | ∠1,∠2,∠7,∠8 |
| অনুরূপ কোণ জোড়া | ∠1 এবং ∠5, ∠2 এবং∠6 ∠3 এবং ∠7, 24 এবং ∠8 |
| অন্তঃস্থ একান্তর কোণ জোড়া | ∠3 এবং ∠6, ∠4 এবং∠5 |
| বহিঃস্থ একান্তর কোণ জোড়া | ∠1 এবং ∠8, ∠2 এবং ∠7 |
| ছেদকের একই পাশের অন্তঃস্থ কোণ জোড়া | ∠3 এবং ∠5, ∠4 এবং∠6 |
অনুরূপ কোণগুলোর বৈশিষ্ট্য: (ক) কোণের কৌণিক বিন্দু আলাদা (খ) ছেদকের একই পাশে অবস্থিত।
একান্তর কোণগুলোর বৈশিষ্ট্য: (ক) কোণের কৌণিক বিন্দু আলাদা (খ) ছেদকের বিপরীত পাশে অবস্থিত
(গ) সরলরেখা দুটির মধ্যে অবস্থিত।
কাজ ১। (ক) চিত্রের কোণগুলো জোড়ায় জোড়ায় শনাক্ত কর। (খ) ∠3 ও ∠6 এর অনুরূপ কোণ দেখাও। (গ) ∠4 এর বিপ্রতীপ কোণ এবং ∠1 এর সম্পূরক কোণ নির্দেশ কর।  |
আমরা জেনেছি যে, একই সমতলে অবস্থিত দুটি সরলরেখা একে অপরকে ছেদ না করলে সেগুলো সমান্তরাল সরলরেখা। দুটি সমান্তরাল সরলরেখা থেকে যেকোনো দুটি রেখাংশ নিলে, রেখাংশ দুটিও পরস্পর সমান্তরাল হয়। দুটি সমান্তরাল সরলরেখার একটির যেকোনো বিন্দু থেকে অপরটির লম্বদূরত্ব সর্বদা সমান। আবার দুটি সরলরেখার একটির যেকোনো দুটি বিন্দু থেকে অপরটির লম্ব দূরত্ব পরস্পর সমান হলেও রেখাদ্বয় সমান্তরাল। এই লম্বদূরত্বকে দুটি সমান্তরাল রেখাদ্বয়ের দূরত্ব বলা হয়। l ও দুটি সমান্তরাল সরলরেখা।
লক্ষ করি, কোনো নির্দিষ্ট সরলরেখার উপর অবস্থিত নয় এরূপ বিন্দুর মধ্য দিয়ে ঐ সরলরেখার সমান্তরাল করে একটি মাত্র সরলরেখা আঁকা যায়।
উপরের চিত্রে, AB ও CD দুটি সমান্তরাল সরলরেখা এবং EF' সরলরেখাগুলোকে যথাক্রমে দুটি বিন্দু Pওতে ছেদ করেছে। EF সরলরেখা AB ও CD সরলরেখাদ্বয়ের ছেদক। ছেদকটি AB ও CD সরলরেখা দুটির সাথে ∠1,∠2,∠3,∠4,∠5,∠6.∠7.∠8 মোট আটটি কোণ তৈরি করেছে। এ কোণগুলোর মধ্যে
(ক) ∠ 1 এবং ∠ 5 , ∠ 2 এবং ∠ 6 , ∠ 3 এবং ∠ 7 , ∠ 4 এবং ∠ 8 পরস্পর অনুরূপ কোণ।
(খ) ∠ 3 এবং ∠ 6 ∠ 4 এবং ∠ 5 হলো পরস্পর একান্তর কোণ।
(গ) ∠ 3 ∠ 4 ∠ 5 ∠ 6 অন্তঃস্থ কোণ।
এই একান্তর ও অনুরূপ কোণগুলোর মধ্যে সম্পর্ক রয়েছে। এই সম্পর্ক বের করার জন্য দলগতভাবে নিচের কাজটি কর।
কাজ: ১। রুলটানা একপৃষ্ঠা কাগজে চিত্রের ন্যায় দুটি সমান্তরাল সরলরেখা ও এদের একটি ছেদক আঁক। দুই জোড়া অনুরূপ কোণ চিহ্নিত কর। প্রতিজোড়া অনুরূপ কোণ সমান কিনা যাচাই কর। সমান হয়েছে কি? ২। দুই জোড়া একান্তর কোণ চিহ্নিত কর। প্রতি জোড়া একান্তর কোণ সমান কিনা যাচাই কর। সমান হয়েছে কি? ৩। সমান্তরাল সরলরেখাদ্বয়ের ছেদকের একই পাশের অন্তঃস্থ কোণ দুটি পরিমাপ কর। কোণ দুটির পরিমাপের যোগফল বের কর। যোগফল তোমার সহপাঠীদের বের করা যোগফলের সাথে তুলনা কর। তোমাদের যোগফল সামান্য কম-বেশি 180° কিন্তু হয়েছে কি?  |
কাজের ফলাফল পর্যালোচনা করে আমরা নিচের সিদ্ধান্তে উপনীত হই:
|
সমান্তরাল সরলরেখার এই তিনটি ধর্ম (property) আলাদাভাবে প্রমাণ করা যায় না। এরা প্রত্যেকেই ইউক্লিডের ৫ম স্বীকার্যের বিভিন্ন রূপ। এদের যেকোনো একটিকে সমান্তরাল সরলরেখার সংজ্ঞা হিসেবে বিবেচনা করলে বাকি দুটি ধর্ম ব্যাখ্যা করা যায়। অর্থাৎ, যদি এই তিনটি ধর্মের যেকোনো একটিকে সত্য ধরে অপর দুটি ধর্মকে ব্যাখ্যা করা যায়, তবে প্রথমে বিবেচিত সংজ্ঞাটিকে আমরা সঠিক বলে ধরে নিতে পারি
সমান্তরাল সরলরেখার একটি ধর্ম: দুটি সমান্তরাল সরলরেখার একটি ছেদক দ্বারা উৎপন্ন প্রত্যেক অনুরূপ কোণ জোড়া সমান-কে সত্য ধরে নিয়ে সমান্তরাল সরলরেখার আরেকটি ধর্মকে নিচে ব্যাখ্যা করা হলো।
দুটি সমান্তরাল সরলরেখার একটি ছেদক দ্বারা উৎপন্ন একান্তর কোণের সম্পর্ক:
দুটি সমান্তরাল সরলরেখাকে একটি সরলরেখা ছেদ করলে একান্তর কোণ জোড়া সমান।
বিশেষ নির্বচন: মনে করি, AB || CD এবং PQ ছেদক তাদের যথাক্রমে E ও F বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, ∠LAEF = একান্তর ∠EFD
প্রমাণ:
ধাপ:
(১) ∠PEB = অনুরূপ ∠EFD
(২) ∠PEB = বিপ্রতীপ ∠AEF
∴ ∠AEF = ∠EFD
[প্রমাণিত]
যথার্থতা
[সমান্তরাল রেখার সংজ্ঞানুসারে অনুরূপ কোণ সমান]
[বিপ্রতীপ কোণদ্বয় পরস্পর সমান। [(১) ও (২) থেকে
| কাজ ১। প্রমাণ কর যে, দুটি সমান্তরাল সরলরেখার একটি ছেদক দ্বারা উৎপন্ন ছেদকের একই পাশের অন্তস্থ কোণদ্বয়ের সমষ্টি দুই সমকোণের সমান। |
চিত্রে, AB || CD এবং PQ ছেদক তাদের যথাক্রমে Eও F বিন্দুতে ছেদ করেছে।
সুতরাং, (ক)∠PEB = অনুরূপ ∠EFD
(খ) ∠AEF = একান্তর ∠EFD
(গ) ∠BEF + ∠EFD = দুই সমকোণ।
কাজ ১। একটি সরলরেখার উপর দুটি বিন্দু নাও। রেখাটির বিন্দু দুটিতে একই দিকে 60° এর সমান দুটি কোণ আঁক। কোণদ্বয়ের অঙ্কিত বাহু দুটি সমান্তরাল কিনা যাচাই কর। ২। 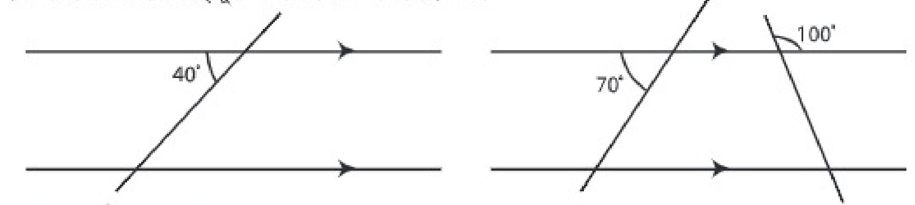 চিত্রে ছেদক দ্বারা উৎপন্ন কোণগুলোর মান বের কর। |
|
চিত্রে, AB ও CD রেখাদ্বয়কে PQ রেখা যথাক্রমে Eও F বিন্দুতে ছেদ করেছে এবং
(ক) ∠AEF = একান্তর ∠EFD
অথবা, (খ) ∠PEB = অনুরূপ ∠EFD
অথবা, (গ) ∠BEF + ∠EFD = দুই সমকোণ।
সুতরাং, AB ও CD রেখা দুটি পরস্পর সমান্তরাল।
১।
চিত্রে, ∠PQR = 55°, ∠LRN = 90° এবং PQ || MR হলে, ∠MRN এর মান নিচের কোনটি?
ক. 35°
খ. 45°
গ. 55°
ঘ. 90°
২।
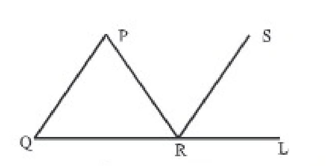
চিত্র, PQ || SR, PQ = PR এবং ∠PRQ=50° হলে, ∠LRS এর মান নিচের কোনটি?
ক. 80°
খ. 75°
গ. 55°
ঘ. 50°
৩।
AB || CD || EF
(১) ∠ x এর মান নিচের কোনটি?
ক. 28°
খ. 32°
গ. 45°
ঘ. 58°
(২) ∠ z এর মান নিচের কোনটি?
ক. 58°
খ. 103°
গ. 122°
ঘ. 148°
(৩) নিচের কোনটি y-z এর মান?
ক. 58°
খ. 77°
গ. 103°
ঘ. 122°
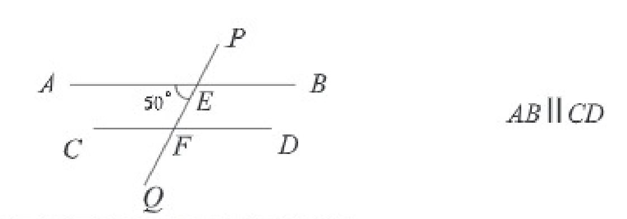
চিত্রের আলোকে ৪ এবং ৫ নম্বর প্রশ্নের উত্তর দাও।
৪। ∠PEA= কত ডিগ্রি?
(ক) 40°
(খ) 50°
(গ) 90°
(ঘ) 130°
৫। ∠EFD এর মান কত?
(ক) 30°
(খ) 40°
(গ) 50°
(ঘ) 90°
৬। ABC ত্রিভুজে ∠B+∠C=90° হলে ∠A = কত ডিগ্রি?
(ক) 90°
(খ) 110°
(গ) 120°
(ঘ) 160°
৭। ≅ চিহ্ন দ্বারা কী বুঝায়?
(ক) সমান
(খ) সর্বসম
(গ) সমান্তরাল
(ঘ) লম্ব
নিচের তথ্যের আলোকে ৮ ও ৯ নং প্রশ্নের উত্তর দাও।
৮। x = কত?
(ক) 75°
(খ) 55°
(গ) 50°
(ঘ) 45°
৯। x + y = কত?
(ক) 160°
(খ) 125°
(গ) 100°
(ঘ) 85°
১০।
চিত্রে, ABIICD, ∠BPE = 60° এবং PQ = PR.
ক. দেখাও যে, ∠APE = 60°
খ. ∠CQF এর মান বের কর।
গ. প্রমাণ কর যে, PQR একটি সমবাহু ত্রিভুজ।
common.read_more
common.or
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
