মনে করি, সোহাগ কোনো দোকান থেকে ১০ টাকা দিয়ে একটি চিপসের প্যাকেট এবং ২৫ টাকা দিয়ে ১ কেজি লবণ কিনল। এখানে লবণ ও চিপস্ এর দামের অনুপাত= ২৫ : ১০ বা ৫ : ২।
আবার, সোহাগদের শ্রেণিতে শিক্ষার্থীর সংখ্যা ৭০। এদের মধ্যে ছাত্র ৫০জন এবং ছাত্রী ২০জন। এখানে ছাত্র ও ছাত্রীসংখ্যার অনুপাত= ৫০ : ২০ বা ৫ : ২। উভয়ক্ষেত্রে অনুপাত দুটি সমান।
অতএব, আমরা বলতে পারি, ২৫ : ১০ = ৫০ : ২০। এই অনুপাতে ৪টি রাশি আছে। এই ৪টি রাশির একটি সমানুপাত তৈরি করেছে।
এর মধ্যে ১ম রাশি ২৫, ২য় রাশি ১০, ৩য় রাশি ৫০ এবং ৪র্থ রাশি ২০ হিসেবে বিবেচনা করলে আমরা লিখতে পারি,
| ১ম রাশি : ২য় রাশি : ৩য় রাশি : ৪র্থ রাশি। |
| চারটি রাশির ১ম ও ২য় রাশির অনুপাত এবং ৩য় ও ৪র্থ রাশির অনুপাত পরস্পর সমান হলে, রাশি চারটি একটি সমানুপাত তৈরি করে। সমানুপাতের প্রত্যেক রাশিকে সমানুপাতী বলে। |
সমানুপাতের ১ম ও ২য় রাশি সমজাতীয় এবং ৩য় ও ৪র্থ রাশি সমজাতীয় হবে।
অর্থাৎ ৪ টি রাশি সমজাতীয় হওয়ার প্রয়োজন নেই। প্রত্যেক অনুপাতের রাশি দুইটি সমজাতীয় হলেই সমানুপাত তৈরি হয়।
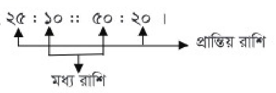
সমানুপাতের ১ম ও ৪র্থ রাশিকে প্রান্তীয় রাশি এবং ২য় ও ৩য় রাশিকে মধ্য রাশি বলে। সমানুপাতে '=' চিহ্নের
পরিবর্তে '::' চিহ্নও ব্যবহার করা হয়। অতএব আমরা লিখতে পারি,
বা, ১ম রাশি/২য় রাশি = ৩য় রাশি/৪র্থ রাশি
বা, ১ম রাশি ৪র্থ রাশি = ২য় রাশি ৩য় রাশি
ত্রৈরাশিক
আমরা জানি, ১ম রাশি ৪র্থ রাশি = ২য় রাশি ৩য় রাশি
মনে করি,
১ম, ২য় ও ৩য় রাশি যথাক্রমে ৯, ১৮, ২০।
তবে ৯ ৪র্থ রাশি = ১৮ ২০
৪র্থ রাশি =
৪র্থ রাশি = ৪০
| এভাবে সমানুপাতের তিনটি রাশি জানা থাকলে ৪র্থ রাশি নির্ণয় করা যায়। এই ৪র্থ রাশি নির্ণয় করার পদ্ধতিকে ত্রৈরাশিক বলে। |
লক্ষ করি
উদাহরণ ২। ৩, ৬,৭ এর ৪র্থ সমানুপাতী নির্ণয় কর।
সমাধান : এখানে ১ম রাশি ৩, ২য় রাশি ৬, ৩য় রাশি ৭
আমরা জানি,
১ম রাশি ৪র্থ রাশি = ২য় রাশি ৩য় রাশি
৩ ৪র্থ রাশি = ৬ ৭
বা, ৪র্থ রাশি =
বা, ১৪
নির্ণেয় ৪র্থ সমানুপাতিক ১৪
উদাহরণ ৩। ৮, ৭ এবং ১৪ এর ৩য় রাশি নির্ণয় কর।
সমাধান: এখানে ১ম রাশি ৮, ২য় রাশি ৭ এবং ৪র্থ রাশি ১৪
আমরা জানি,
১ম রাশি ৪র্থ রাশি = ২য় রাশি ৩য় রাশি
বা, ৮ ১৪ = ৭ ৩য় রাশি
৩য় রাশি =
= ১৬
কাজ: নিচের খালি ঘর পূরণ কর। (ক) : ৯ :: ১৬ : ৮ (খ) ৯ : ১৮ :: ২৫ : |
ক্রমিক সমানুপাত
মনে করি, ৫ টাকা, ১০ টাকা ও ২০ টাকা এই তিনটি রাশি দ্বারা ৫: ১০ এবং ১০: ২০ এই দুটি অনুপাত নেওয়া হলো। এখানে, ৫: ১০: ১০: ২০। এ ধরনের সমানুপাতকে ক্রমিক সমানুপাত বলে। ৫ টাকা, ১০ টাকা ও ২০ টাকাকে ক্রমিক সমানুপাতী বলে।
| তিনটি রাশির ১ম ও ২য় রাশির অনুপাত এবং ২য় ও ৩য় রাশির অনুপাত পরস্পর সমান হলে, সমানুপাতটিকে ক্রমিক সমানুপাত বলে। রাশি তিনটিকে ক্রমিক সমানুপাতী বলে। |
ক: খ :: খ গ সমানুপাতটির তিনটি রাশি ক, খ, গ ক্রমিক সমানুপাতী হলে বাক গ = (খ)২ হবে।
অর্থাৎ, ১ম ও ৩য় রাশির গুণফল দ্বিতীয় রাশির বর্গের সমান।
লক্ষ করি:
উদাহরণ ৪। একটি ক্রমিক সমানুপাতের ১ম ও ৩য় রাশি যথাক্রমে ৪ ও ১৬ হলে, মধ্য সমানুপাতী ও ক্রমিক সমানুপাত নির্ণয় কর।
সমাধান: আমরা জানি, ১ম রাশি ৩য় রাশি = (২য় রাশি)২
এখানে, ১ম রাশি = ৪ এবং ৩য় রাশি = ১৬
৪ ১৬ = (মধ্য রাশি)২
অথবা, (মধ্য রাশি)২ = ৬৪
মধ্য রাশি =
নির্ণেয় ক্রমিক সমানুপাত ৪ : ৮ :: ৮ : ১৬ এবং নির্ণেয় মধ্য সমানুপাতী ৮
উদাহরণ ৫। ৫টি খাতার দাম ২০০ টাকা হলে, ৭টি খাতার দাম কত?
সমাধান: এখানে খাতার সংখ্যা বাড়লে দামও বাড়বে।
অর্থাৎ, খাতার সংখ্যার অনুপাত= খাতার দামের অনুপাত
৫ : ৭ = ২০০ টাকা : ৭টি খাতার দাম
বা, = ২০০ টাকা/ ৭টি খাতার দাম
বা, ৭টি খাতার দাম = ৭ ২০০ টাকা / ৫ = ২৮০ টাকা।
উদাহরণ ৬। ১২জন লোক একটি কাজ ৯ দিনে করতে পারে। একই হারে কাজ করলে ১৮জনে কাজটি কত দিনে করতে পারবে?
সমাধান: লক্ষ করি, লোকসংখ্যা বাড়লে সময় কম লাগবে, আবার লোকসংখ্যা কমলে সময় বেশি লাগবে। লোকসংখ্যার সরল অনুপাত সময়ের ব্যস্ত অনুপাতের সমান হবে।
১২ : ১৮ = নির্ণেয় সময় : ৯ দিন
বা, = নির্ণেয় সময় / ৯ দিন
বা নির্ণেয় সময় = দিন = ৬ দিন
সমানুপাতিক ভাগ
মনে করি, ৫০০ টাকা ৩ : ২ অনুপাতে বণ্টন করতে হবে।
এখানে ৩ : ২ অনুপাতের পূর্বরাশি ও উত্তর রাশির যোগফল = ৩+২ = ৫
১ম ভাগ = ৫০০ টাকার অংশ = ৩০০ টাকা
এবং ২য় ভাগ = ৫০০ টাকার অংশ = ২০০ টাকা।
অতএব,
| একটি অংশের পরিমাণ প্রদত্ত রাশি ঐ অংশের আনুপাতিক সংখ্যা / অনুপাতের পূর্ব ও উত্তর রাশির যোগফল |
এভাবে উপরের পদ্ধতিতে একটি রাশিকে বিভিন্ন ভাগে বিভক্ত করা যায়।
| একটি প্রদত্ত রাশিকে একাধিক নির্দিষ্ট সংখ্যার অনুপাতে বিভক্ত করাকে সমানুপাতিক ভাগ বলে। |
উদাহরণ ৭। ২০ মিটার কাপড়কে তিন ভাইবোন অমিত, সুমিত ও চৈতির মধ্যে ৫: ৩ : ২ অনুপাতে ভাগ করলে প্রত্যেকের কাপড়ের পরিমাণ কত?
সমাধান: কাপড়ের পরিমাণ = ২০ মিটার
প্রদত্ত অনুপাত = ৫ : ৩ : ২
অনুপাতের সংখ্যাগুলোর যোগফল = ৫+৩+২ = ১০
অমিতের অংশ = ২০ মিটারের অংশ = ১০ মিটার
সুমিতের অংশ = ২০ মিটারের অংশ = ৬ মিটার
এবং চৈতির অংশ = ২০ মিটারের অংশ = ৪ মিটার
অমিত, সুমিত ও চৈতির কাপড়ের পরিমাণ যথাক্রমে ১০ মিটার, ৬ মিটার ও ৪ মিটার।
কাজ ১। কঃ খ = ৪ : ৫, খঃ গ ৭ : ৯ হলে, ক খ গ নির্ণয় কর। |
উদাহরণ ৮। পনির ও তপনের আয়ের অনুপাত ৪ : ৩। তপন ও রবিনের আয়ের অনুপাত ৫ : ৪। পনিরের আয় ১২০ টাকা হলে, রবিনের আয় কত?
সমাধান: পনির ও তপনের আয়ের অনুপাত ৪ : ৩ = = = = ২০ : ১৫
তপন ও রবিনের আয়ের অনুপাত = = = ১৫ : ১২
পনিরের আয়: তপনের আয় রবিনের আয় = ২০ : ১৫ : ১২
পনিরের আয়: রবিনের আয় = ২০ : ১২
বা, পনিরের আয় / রবিনের আয় =
বা, রবিনের আয় = পনিরের আয় ১২ / ২০ টাকা
= টাকা বা ৭২ টাকা।
রবিনের আয় ৭২ টাকা
common.read_more