আমরা আগের শ্রেণিতে জেনেছি, তিনটি সরলরেখাংশ দ্বারা আবদ্ধ চিত্রকে ত্রিভুজ বলে [চিত্র ১]।

১. চিত্র ১ থেকে দেখা যাচ্ছে, AB, BC ও AC এই তিনটি সরলরেখাংশ দিয়ে একটি ত্রিভুজ ABC গঠিত হয়েছে। তাই AB, BC ও AC এই প্রত্যেকটি রেখাংশই ত্রিভুজ ABC এর বাহু (side)।
| যে তিনটি সরলরেখাংশ দিয়ে ত্রিভুজ গঠিত হয় তাদের প্রত্যেকটিকে ঐ ত্রিভুজের বাহু (side) বলা হয়। |
২. চিত্রে দেখা যাচ্ছে, AB ও AC বাহু দুইটি পরস্পর A বিন্দুতে; AB ও BC বাহু দুটি পরস্পর B বিন্দুতে এবং AC ও BC বাহুদ্বয় পরস্পর C বিন্দুতে ছেদ করেছে। তাই A, B, C এই প্রতিটি বিন্দুকেই ∆ABC এর শীর্ষবিন্দু বলা হয়। ইংরেজি বড়ো হাতের অক্ষর ও শীর্ষবিন্দু দিয়ে ত্রিভুজের নামকরণ করা হয়। যেমন: চিত্রের ত্রিভুজের শীর্ষবিন্দুগুলো হলো A, B, C. তাই চিত্রের ত্রিভুজের নামকরণ ∆ABC করা হয়েছে।
| যেকোনো ত্রিভুজের দুটি বাহু পরস্পর যে বিন্দুতে ছেদ করে সেই বিন্দুকে ঐ ত্রিভুজের শীর্ষবিন্দু (vertex) বলা হয়। ত্রিভুজের শীর্ষবিন্দুর নামানুসারে ত্রিভুজের নামকরণ করা হয়। |
৩. চিত্রে দেখা যাচ্ছে, A, B ও C শীর্ষবিন্দু তিনটিতে যথাক্রমে ∠BAC, ∠ABC ও ∠ACB উৎপন্ন করেছে। এই প্রত্যেকটি কোণকে ∆ABC এর শীর্ষকোণ (vertical angle) বলা হয়। কখনো কখনো এটিকে শিরঃকোণও বলা হয়। যেহেতু যেকোনো ত্রিভুজের শীর্ষবিন্দু তিনটি তাই প্রত্যেকটি ত্রিভুজের তিনটি শীর্ষবিন্দু উৎপন্ন হয়।
| যেকোনো ত্রিভুজের শীর্ষবিন্দুতে যে কোণ উৎপন্ন হয়, তাকে ঐ ত্রিভুজের শীর্ষকোণ বলা হয়। যেহেতু যেকোনো ত্রিভুজের শীর্ষবিন্দু তিনটি তাই প্রত্যেকটি ত্রিভুজের তিনটি শীর্ষকোণ উৎপন্ন হয়। |
মনে করি, ABC যেকোনো একটি ত্রিভুজ, যার A, B ও C তিনটি শীর্ষবিন্দুতে উৎপন্ন কোণগুলো যথাক্রমে ∠BAC, ∠ABC ও ∠ACB এবং বাহু তিনটি হলো AB, BC ও AC।
এখন ∆ABC এর তিনটি বাহু AB, BC ও AC এর মধ্য বিন্দুগুলো যথাক্রমে D, E ও F নির্ণয় করি [চিত্র ২] এবং প্রতিটি বাহুর মধ্য বিন্দু ও তার বিপরীত শীর্ষবিন্দু সংযোগ করি। এতে ∆ABC এ AD, BE ও CF এই তিনটি সরলরেখাংশ পাওয়া যাচ্ছে। AD, BE ও CF এই তিনটি রেখাংশের প্রত্যেকটিকে ∆ABC এর মধ্যমা বলা হয়।
| যেকোনো ত্রিভুজের যেকোনো শীর্ষবিন্দু থেকে তার বিপরীত বাহুর মধ্যবিন্দুর সংযোগ সরলরেখাংশকে ঐ ত্রিভুজের মধ্যমা বলা হয়। |
মনে করি, ABC যেকোনো একটি ত্রিভুজ, যার A. B ও C তিনটি শীর্ষবিন্দু এবং তার তিনটি বাহ AB. BC ও AC। এখন ∆ABC এর তিনটি শীর্ষবিন্দু A, B ও C থেকে তার বিপরীত বাহুর উপর বা বর্ধিতাংশের উপর লম্ব আঁকি
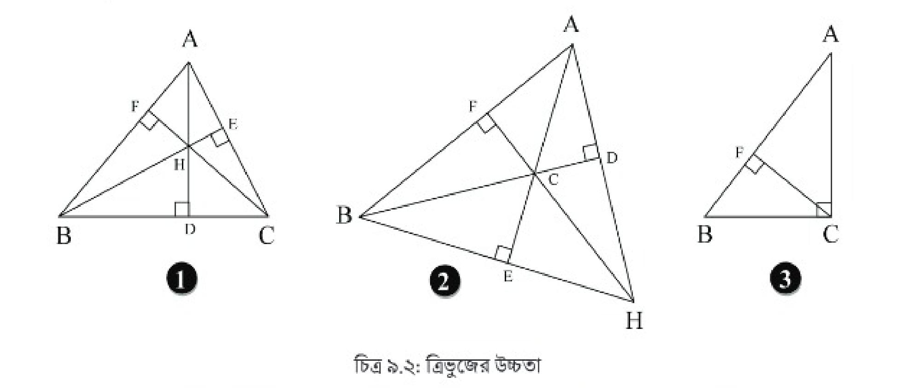
১. চিত্র ৯.২ (1) থেকে দেখা যাচ্ছে যে, ∆ABC এর তিনটি শীর্ষবিন্দু A, B, C হতে তাদের বিপরীত বাহু যথাক্রমে BC, AC, AB এর উপর AD, BE, CF লম্ব আঁকা সম্ভব হয়েছে।
২. চিত্র ৯.২ (2) থেকে দেখা যাচ্ছে যে, ∆ABC এর শীর্ষবিন্দু C হতে এর বিপরীত বাহু AB এর উপর CF লম্ব আঁকা সম্ভব হয়েছে। কিন্তু শীর্ষবিন্দু A ও B হতে তাদের বিপরীত বাহু যথাক্রমে BC, AC এর উপর AD, BE লম্ব আঁকা সম্ভব হয়নি। তবে BC ও AC বাহুর বর্ধিতাংশের উপর AD, BE লম্ব আঁকা সম্ভব হয়েছে।
৩. চিত্র ৯.২ (3) থেকে দেখা যাচ্ছে যে, ∆ABC এর তিনটি শীর্ষবিন্দু A, B, C হতে তাদের বিপরীত বাহ যথাক্রমে BC, AC ও AB এর উপর AD, BE ও CF লম্ব আঁকা সম্ভব হয়েছে। তবে A ও B থেকে তার বিপরীত বাহু যথাক্রমে BC ও AC এর উপর AC ও BC নিজেরাই লম্ব।
একটি ত্রিভুজের তিনটি শীর্ষবিন্দু থাকে। তাই শীর্ষবিন্দুগুলো থেকে বিপরীত বাহুর উপর বা তার বর্ধিতাংশের উপর তিনটি লম্ব আঁকা যায়। এই প্রত্যেকটি লম্বকেই ABC ত্রিভুজের উচ্চতা বলা যায়। তবে যে বাহকে ভূমি বিবেচনা করা হয় সেই বাহুর বা বাহুর বর্ধিতাংশের উপরের লম্বকেই ঐ ত্রিভুজের উচ্চতা বিবেচনা করা হয়।
| যেকোনো ত্রিভুজের ভূমির বিপরীত শীর্ষবিন্দু হতে ভূমির উপর বা ভূমির বর্ধিতাংশের উপর অঙ্কিত লম্বকে ঐ ত্রিভুজের উচ্চতা বলা হয়। আর কোনো ত্রিভুজের যে বিন্দুতে উচ্চতা বা তার বর্ধিতাংশ তিনটি পরস্পরকে ছেদ করে সেই বিন্দুকে লম্ববিন্দু বলা হয়। |
ধরি, যেকোনো একটি ত্রিভুজ ABC, যার তিনটি বাহু AB, BC ও AC।

উপরের চিত্রের ∆ABC এর ভিতরের দিকে তিনটি শীর্ষবিন্দুতে ∠BAC, ∠ABC ও ∠ACB উৎপন্ন করেছে। এই কোণ তিনটিকে ত্রিভুজের অন্তঃস্থকোণ বলা হয়।
| যেকোনো ত্রিভুজের তিনটি শীর্ষবিন্দুতে ত্রিভুজের ভিতরের দিকে যে তিনটি কোণ উৎপন্ন হয় তাদেরকে ত্রিভুজের অন্তঃস্থকোণ বলা হয়। |
মনে করি, যেকোনো একটি ত্রিভুজ ABC, যার তিনটি বাহ AB, BC ও AC এবং তিনটি কোণ ∠ABC, ∠ACB ও ∠BAC। এখন ∆ABC এর যেকোনো একটি বাহু BC কে D পর্যন্ত বর্ধিত করি । এতে ∆ABC এর বাইরের দিকে ∠ACD উৎপন্ন হয়েছে। এই কোণকে কী কোণ বলব?

∆ABC এর ∠ABC, ∠ACB ও ∠BAC কে অন্তঃস্থ কোণ বলা হয়। আর ∠ACD কে বহিঃস্থ কোণ বলা হয়।
| যেকোনো ত্রিভুজের যেকোনো বাহকে যেকোনো দিকে বর্ধিত করলে বাইরের দিকে যে কোণ উৎপন্ন হয় তাকে ঐ ত্রিভুজের বহিঃস্থ কোণ বলা হয়। |
উপরের চিত্রে দেখা যাচ্ছে, বহিঃস্থ ∠ACD এর সন্নিহিত কোণ হলো ∠ACB। কিন্তু ∠ABC ও ∠BAC কোণ দুটিকে কী কোণ বলব?
∆ABC এ, ∠ABC ও ∠BAC কোণ দুটিকে বহিঃস্থ ∠ACD এর অন্তঃস্থ বিপরীত কোণ বলা হয়।
| যেকোনো ত্রিভুজের বহিঃস্থ কোণের সন্নিহিত কোণ ছাড়া ত্রিভুজের অভ্যন্তরে যে দুটি কোণ থাকে তাদেরকে ঐ বহিঃস্থ কোণের অন্তঃস্থ বিপরীত কোণ বলা হয়। |
মনে করি, যেকোনো একটি ত্রিভুজ ABC, যার তিনটি কোণ ∠ABC, ∠ACB ও ∠BAC। এখানে △ABC এর তিনটি কোণের সমষ্টি অর্থাৎ (∠ABC+∠ACB + ∠BAC) নির্ণয় করতে হবে
অঙ্কন: A বিন্দু দিয়ে BC || PQ আঁকি।

চিত্র থেকে দেখা যাচ্ছে, BC || PQ এবং এদের ছেদক AB। তাই ছেদক বিপরীত পাশে উৎপন্ন ∠ABC ও ∠PAB একান্তর কোণ দুটি সমান। অর্থাৎ ∠ABC = ∠PAB = x ... (i)
আবারো দেখা যাচ্ছে, BC || PQ এবং এদের ছেদক AC। তাই ছেদকের বিপরীত পাশে উৎপন্ন ∠ACB ও ∠QAC একান্তর কোণ দুটি সমান। অর্থাৎ ∠ACB = ∠QAC = y ... (ii)
আবার PQ রেখার A বিন্দুতে AB রেখা ছেদ করায় ∠BAP ও ∠BAQ দুইটি সন্নিহিত কোণ উৎপন্ন করেছে। তাই আমরা লিখতে পারি:
∠BAP + ∠BAQ = 180°
∠BAP + ∠BAC + ∠CAQ = 180° [∠BAC + ∠CAQ = ∠BAQ]
ZABC+∠BAC + ∠ACB = 180°
অর্থাৎ ∆ABC এর তিনটি অন্তঃস্থ কোণের সমষ্টি 180° বা দুই সমকোণ।
| যেকোনো ত্রিভুজের তিনটি অন্তঃস্থ কোণের সমষ্টি 180° এবা দুই সমকোণ। এটা ইউক্লিডের প্রতিজ্ঞা ৩২। |
common.read_more