আমাদের চারদিকে বিভিন্ন আকৃতি (shape) ও আকার (size) এর বস্তু দেখতে পাই। তাই এই দুটি জিনিস নিয়ে পরিষ্কার ধারণা থাকা দরকার। তাই নিচের চিত্রগুলো ভালো করে দেখি।

১. চিত্র 1 ও 2 এর আকৃতি ভিন্ন ভিন্ন কিন্তু আকার একই। অর্থাৎ ছবি দুটি পরিমাপের দৃষ্টিতে সমান কিন্তু দেখতে আলাদা।
২. চিত্র 3 ও 4 এর আকৃতি একই কিন্তু আকার ভিন্ন ভিন্ন। অর্থাৎ ছবি দুটি দেখতে একই রকম কিন্তু পরিমাপের দৃষ্টিতে আলাদা। এই ধরনের জিনিসগুলোকে পরস্পরের সদৃশ বলা হয়।
৩. চিত্র 5 ও 6 এর আকৃতি ও আকার উভয়ই একই। অর্থাৎ ছবি দুটি দেখতে একই রকম এবং পরিমাণগত দিক থেকেও সমান। তাই এরা দেখতে হুবহু সমান। এই ধরনের জিনিসগুলোকে পরস্পরের সর্বসম বলা হয়।
এই অধ্যায়ে আমরা জ্যামিতির দুটি অত্যন্ত গুরুত্বপূর্ণ ধারণা- সর্বসমতা ও সদৃশতা নিয়ে আলোচনা করব। তবে আমরা শুধুমাত্র সমতলীয় সর্বসমতা ও সদৃশতা মধ্যেই আলোচনা সীমিত রাখব।
নিচের সমতলীয় চিত্রগুলো দেখে তাদের আকার ও আকৃতি নিয়ে আলোচনা করি।
১. পুরোপুরি ঢাকা হচ্ছে, কোনো ছোটো জিনিসকে তারচেয়ে বড় জিনিস দিয়ে ঢেকে দেওয়া। এখানে চিত্র ২-এ দেখা যাচ্ছে, ABCD তলের সম্পূর্ণ অংশকে EFGH তল দ্বারা ঢাকা হয়েছে। বিপরীতভাবে বলা যায় EFGH তলের কিছু অংশকে ABCD তল দ্বারা ঢাকা হয়েছে। তাই বলা যায়, এই দুটি চিত্র আকৃতিতে একই হলেও আকারে ভিন্ন ভিন্ন। একারণে ABCD ও EFGH সর্বসম নয়।
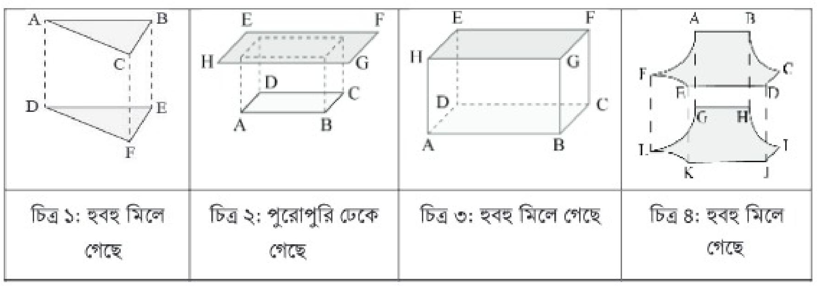
২. হবহু ঢাকা বা সর্বতোভাবে মিলার যাওয়ার অর্থ হচ্ছে, কোনো একটি জিনিসের প্রতিটি বিন্দুর সাথে অন্য একটি জিনিস মিলে যাওয়া। এখানে চিত্র ১, ৩, ৪ থেকে যথাক্রমে দেখা যাচ্ছে, ABC তলটি DEF দ্বারা, ABCD তলটি EFGH দ্বারা ও ABCDEF তলটি GHIJKL দ্বারা হুবহু ঢেকে বা সর্বতোভাবে মিলে গেছে। তাই এই চিত্রগুলোর আকৃতি ও আকার উভয়ই একই। একারণে এগুলো সর্বসম ও সর্বদা সমান।
৩. চিত্র ৩ থেকে দেখা যাচ্ছে, AB রেখাংশটি GH রেখাংশ দ্বারা হুবহু ঢেকে বা সর্বতোভাবে মিলে গেছে তাই AB ও GH পরস্পর সর্বসম। আবার চিত্র ২ থেকে দেখা যাচ্ছে, AB রেখাংশটি GH দ্বারা আংশিকভাবে ঢেকে গেছে AB ও GH পরস্পর সর্বসম নয় এবং দৈর্ঘ্যও অসমান। সুতরাং বলা যায়, দুটি রেখাংশের দৈর্ঘ্য সমান হলেই তারা পরস্পর সর্বসম হবে।
৪. চিত্র ৫ ও ৬ থেকে যথাক্রমে দেখা যাচ্ছে, ∠ABC = 40° ও ∠DEF = 40° তাই ∠ABC = ∠DEF অর্থাৎ কোণ দুটির মান সমান। দুটো কোণের মান সমান হলে তাদের পরস্পরকে হুবহু ঢাকা বা সর্বতোভাবে মিলে যায়। একারণে তারা পরস্পর সর্বসম ও সমান। আবার চিত্র ৬ ও ৭ থেকে যথাক্রমে দেখা যাচ্ছে, ∠DEF = 40° ∠RST = 60° অর্থাৎ কোণ দুটির মান অসমান। তাই দুটি কোণের মান অসমান হওয়ায় তারা পরস্পরকে হবহু ঢাকা বা সর্বতোভাবে মিলে যাচ্ছে না। এ কারণে তারা পরস্পর সর্বসম নয় ও তারা পরস্পর অসমান।

উপরের উদাহরণগুলো থেকে বলা যায়, একটি বস্তুর সাথে অপর একটি বস্তু দ্বারা হুবহু ঢাকা বা সর্বতোভাবে মিলে যায়, তাহলে ঐ বস্তু দুটিকে পরস্পরের সর্বসম বলা হয়।
| যখন একটি বস্তুর সাথে অপর একটি বস্তু দ্বারা হৰহ ঢাকা বা সর্বতোভাবে মিলে যায়, তখন ঐ বস্তু দুটিকে পরস্পরের সর্বসম বলা হয়। অন্যভাবে, যখন দুটি বস্তুর আকৃতি ও আকার উভয়ই একই রকম হয়, তখন সেই বস্তু দুটিকে সর্বসম বলা হয়। |
এখন যদি ABCD ও EFGH পরস্পর সর্বসম হয়, তহলে আমরা ABCD = EFGH এভাবে লিখে প্রকাশ করি। এর অর্থ হলো ABCD ও EFGH পরস্পর সর্বসম।
১. পরের পৃষ্ঠার চিত্র ১ থেকে দেখা যাচ্ছে, ∆ABC ও △DEF পরস্পরের সাথে হুবহু বা সর্বতোভাবে মিলে গেছে এবং দুটি ত্রিভুজের আকার ও আকৃতি উভয়ই একই রকমের হয়, তাই ত্রিভুজ দুটিকে সর্বসম বলা হয়।
অন্যভাবে বলা যায়, একটি ত্রিভুজ দিয়ে অন্য আরেকটি ত্রিভুজকে যদি হুবহু বা সর্বতোভাবে মিলে যায়, তাহলে ত্রিভুজ দুটিকে সর্বসম বলা হয়। এখানে হবহু বা সর্বতোভাবে মিলে যাওয়ার অর্থ হলো কোনো একটি ত্রিভুজের প্রতিটি বিন্দুর সাথে অন্য একটি ত্রিভুজের প্রতিটি বিন্দুর হুবহু বা সর্বতোভাবে মিলে যাওয়া বুঝায়। তাই দুটি ত্রিভুজ যদি সর্বসম হয়, তাহলে ঐ ত্রিভুজ দুটির অনুরূপ বাহুগুলো ও অনুরূপ কোণগুলো পরস্পর সমান হয়ে যায়।

১. উপরের চিত্র ২ থেকে দেখা যাচ্ছে, ∆ABC ও ∆DEF পরস্পরের সাথে হবহু বা সর্বতোভাবে মিলে যায়নি এবং দুটি ত্রিভুজের আকৃতি একই হলেও আকার ভিন্ন ভিন্ন ত্রিভুজ দুটি সর্বসম নয়।
| দুটি ত্রিভুজের যদি আকার ও আকৃতি উভয়ই একই রকমের হয়, তাহলে ত্রিভুজ দুটিকে সর্বসম বলা হয়। আর যদি দুটি ত্রিভুজ সর্বসম হয়, তাহলে ঐ ত্রিভুজ দুটির অনুরূপ বাহুগুলো ও অনুরূপ কোণগুলো পরস্পর সমান হয়ে যায়। |
এখন যদি ∆ABC ও △DEF পরস্পর সর্বসম হয়, তহলে আমরা ∆ABC = ∆DEF এভাবে লিখে প্রকাশ করি। এর অর্থ হলো ∆ABC ও △DEF পরস্পর সর্বসম।
এবার ত্রিভুজের সর্বসমতা প্রমাণের জন্য কী তথ্য প্রয়োজন? এ জন্য দলগতভাবে নিচের কাজটি কর:
| কাজ: ১. ∆ABC ও ∆DEF দুটি ত্রিভুজ আঁক, যাদের AB = DE = 5 সেমি, BC = EF = 6 সেমি এবং ∠ABC = ∠DEF = 60°1 ২. ত্রিভুজ দুটির তৃতীয় বাহুর দৈর্ঘ্য এবং অন্য কোণ দুটি পরিমাপ কর। ৩. তোমাদের পরিমাপগুলো তুলনা কর। এখান থেকে কি কিছু দেখতে পাচ্ছ? |
common.read_more