[এই অধ্যায়ের প্রয়োজনীয় পূর্বজ্ঞান বইয়ের শেষে পরিশিষ্ট অংশে সংযুক্ত আছে। প্রথমে পরিশিষ্ট অংশ পাঠ/আলোচনা করতে হবে।]
আমরা জেনেছি, তিনটি রেখাংশ দ্বারা আবদ্ধ ক্ষেত্রের সীমারেখাকে ত্রিভুজ বলা হয় এবং রেখাংশগুলোকে ত্রিভুজের বাহু বলে। যেকোনো দুটি বাহুর সাধারণ বিন্দুকে শীর্ষবিন্দু বলা হয়। দুটি বাহু শীর্ষবিন্দুতে যে কোণ উৎপন্ন করে তা ত্রিভুজের একটি কোণ। ত্রিভুজের তিনটি বাহু ও তিনটি কোণ আছে। বাহুভেদে ত্রিভুজ তিন প্রকার: সমবাহু, সমদ্বিবাহু ও বিষমবাহু। আবার কোণভেদেও ত্রিভুজ তিন প্রকার: সূক্ষ্মকোণী, স্থূলকোণী ও সমকোণী। ত্রিভুজের বাহু তিনটির দৈর্ঘ্যের সমষ্টিকে ত্রিভুজের পরিসীমা বলা হয়। এর আলোকে ত্রিভুজের অন্যান্য বৈশিষ্ট্য এবং ত্রিভুজ সংক্রান্ত মৌলিক উপপাদ্য ও অঙ্কন বিষয়ে আলোচনা করা হয়েছে।
অধ্যায় শেষে শিক্ষার্থীরা -
পাশের চিত্রে, ABC একটি ত্রিভুজ। A, B, C ত্রিভুজটির তিনটি শীর্ষবিন্দু। AB, BC, CA ত্রিভুজটির তিনটি বাহু এবং ∠A, ∠B, ∠C তিনটি কোণ। ত্রিভুজটির যেকোনো একটি বাহু BC এর মধ্যবিন্দু D নির্ণয় করি এবং D হতে বিপরীত শীর্ষবিন্দু A পর্যন্ত রেখাংশ আঁকি। AD, ABC ত্রিভুজের একটি মধ্যমা।

| ত্রিভুজের শীর্ষবিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত অঙ্কিত রেখাংশ মধ্যমা। |
পাশের চিত্রে, ABC একটি ত্রিভুজ। A শীর্ষবিন্দু হতে বিপরীত বাহু BC এর লম্ব দূরত্বই ত্রিভুজের উচ্চতা। A হতে BC এর উপর লম্ব AM অঙ্কন করি। AM, ABC ত্রিভুজের উচ্চতা। এভাবে প্রত্যেক শীর্ষবিন্দু হতে ত্রিভুজের উচ্চতা নির্ণয় করা যায়।

কোনো ত্রিভুজের একটি বাহু বর্ধিত করলে যে কোণ উৎপন্ন হয় তা ত্রিভুজটির একটি বহিঃস্থ কোণ। এই কোণের সন্নিহিত কোণটি ছাড়া ত্রিভুজের অপর দুটি কোণকে এই বহিঃস্থ কোণের বিপরীত অন্তঃস্থ কোণ বলা হয়। পাশের চিত্রে, ∆ABC এর BC বাহুকে D পর্যন্ত বর্ধিত করা হয়েছে। ∠ACD ত্রিভুজটির একটি বহিঃস্থ কোণ। ∠ABC, ∠BAC ও ∠ACB ত্রিভুজটির তিনটি অন্তঃস্থ কোণ। ∠ACB কে ∠ACD এর পরিপ্রেক্ষিতে সন্নিহিত অন্তঃস্থ কোণ বলা হয়। ∠ABC ও BAC এর প্রত্যেককে ∠ACD এর বিপরীত অন্তঃস্থ কোণ বলা হয়।

কাজ ১। ত্রিভুজের কয়টি মধ্যমা? কয়টি উচ্চতা? ২। মধ্যমা ও উচ্চতা কি সর্বদাই ত্রিভুজের অভ্যন্তরে থাকবে? ৩। একটি ত্রিভুজ আঁক, যার উচ্চতা ও মধ্যমা একই রেখাংশ। |
কোণগুলোকে নিয়ে ত্রিভুজের একটি অসাধারণ ধর্ম রয়েছে। নিচের তিনটি কাজ করি এবং ফলাফল পর্যবেক্ষণ করি।
কাজ:  ২। একটি ত্রিভুজ আঁক এবং এর অনুরূপ আরও দুটি ত্রিভুজ আঁক। ত্রিভুজ তিনটি চিত্রের মত করে সাজাও। কোণ তিনটি একত্রে সরল কোণ তৈরি করে কি?  ৩। খাতায় তোমার পছন্দ মতো তিনটি ত্রিভুজ অঙ্কন কর। চাঁদার সাহায্যে প্রতিটি ত্রিভুজের কোণগুলো পরিমাপ কর এবং নিচের সারণিটি পূরণ কর। (একটি করে দেখানো হলো)
প্রতিটি ক্ষেত্রে কোণ তিনটির যোগফল মোটামুটি 180° হয়েছে কি? |
উপপাদ্য ১। ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণের সমান।

বিশেষ নির্বচন: মনে করি, ABC একটি ত্রিভুজ।
প্রমাণ করতে হবে যে, ∠BAC+∠ABC+∠ACB = দুই সমকোণ।
অঙ্কন: BC বাহুকে D পর্যন্ত বর্ধিত করি এবং BA রেখার সমান্তরাল করে CE রেখা আঁকি।
প্রমাণ:
| ধাপ | যথার্থতা |
(১) ∠BAC =∠ACE [BACE এবং AC রেখা তাদের ছেদক।]
[∵ একান্তর কোণ দুটি সমান।]
(২) ∠ABC = ∠ECD [BACE এবং BD রেখা তাদের ছেদক।]
[∵ অনুরূপ কোণ দুটি সমান।।
(৩) ∠BAC+∠ABC = ∠ACE+∠ECD = ∠ACD
(8) ∠BAC+∠ABC+∠ACB = ∠ACD + ∠ACB [উভয়পক্ষে ∠ACB যোগ করে]
(৫) ∠ACD+∠ACB = দুই সমকোণ [সরল কোণ উপপাদ্য]
∴ ∠BAC+∠ABC + ∠ACB = দুই সমকোণ। [প্রমাণিত]
অনুসিদ্ধান্ত ১। ত্রিভুজের একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা এর বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান।
অনুসিদ্ধান্ত ২। ত্রিভুজের একটি বাহুকে বর্ধিত করলে যে বহিঃস্থ কোণ উৎপন্ন হয়, তা এর অন্তঃস্থ বিপরীত কোণ দুটির প্রত্যেকটি অপেক্ষা বৃহত্তর।
অনুসিদ্ধান্ত ৩। সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয় পরস্পর পূরক।
অনুসিদ্ধান্ত ৪। সমবাহু ত্রিভুজের প্রত্যেকটি কোণের পরিমাপ 60°.
১। ∠ABD, ∠CBD এবং ∠ BCD এর মান নির্ণয় কর।

২। একটি সমদ্বিবাহু ত্রিভুজের শীর্ষবিন্দুতে অবস্থিত কোণটির মান 50°। অবশিষ্ট কোণ দুটির মান নির্ণয় কর।
৩। প্রমাণ কর যে, চতুর্ভুজের চারটি কোণের সমষ্টি চার সমকোণের সমান।
81 ∆ABC-এর AC BC; E, AC এর বর্ধিতাংশের উপর যেকোনো বিন্দু এবং ED AB ED এবং BC পরস্পরকে O বিন্দুতে ছেদ করে। প্রমাণ কর যে, ∠CEO = ∠DBO
পাশের চিত্রে ABC একটি ত্রিভুজ। ত্রিভুজটির তিনটি বাহু AB, BC, CA এবং তিনটি কোণ হলো ∠ABC (সংক্ষেপে ∠B), ∠BCA (সংক্ষেপে ∠C) এবং ∠BAC (সংক্ষেপে ∠A)। সাধারণত ∠A, ∠B ও ∠ C এর বিপরীত বাহুগুলোকে যথাক্রমে a, b ও c প্রকাশ করা হয়।
∴ BC=a, CA=b এবং AB=c

ত্রিভুজের বাহু ও কোণের মধ্যে সম্পর্ক রয়েছে। বিষয়টি বোঝার জন্য নিচের কাজটি কর।
| কাজ ১। যেকোনো একটি কোণ আঁক। কোণটির শীর্ষবিন্দু থেকে উভয় বাহুতে সমান দূরত্বে দুটি বিন্দু চিহ্নিত কর। বিন্দু দুটি যুক্ত কর। একটি সমদ্বিবাহু ত্রিভুজ অঙ্কিত হলো। চাঁদার সাহায্যে ভূমি সংলগ্ন কোণ দুটি পরিমাপ কর। কোণ দুটি কি সমান? |
যদি কোনো ত্রিভুজের দুটি বাহু পরস্পর সমান হয়, তবে এদের বিপরীত কোণ দুটিও পরস্পর সমান। পরবর্তী অধ্যায়ে এই প্রতিজ্ঞাটির যুক্তিমূলক প্রমাণ করা হবে। অর্থাৎ, ABC ত্রিভুজে AB = AC হলে, ∠ABC = ∠ACB হবে। সমদ্বিবাহু ত্রিভুজের এ বৈশিষ্ট্য বিভিন্ন যুক্তিমূলক প্রমাণে প্রয়োগ করা হয়।

কাজ ১। যেকোনো তিনটি ত্রিভুজ আঁক। রুলারের সাহায্যে প্রতিটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য ও চাঁদার সাহায্যে তিনটি কোণ পরিমাপ কর এবং নিচের সারণিটি পূরণ কর।
প্রতিটি ক্ষেত্রে কোনো দুটি বাহু ও এদের বিপরীত কোণগুলো তুলনা কর। এ থেকে কী সিদ্ধান্তে উপনীত হওয়া যায়? |
কোনো ত্রিভুজের একটি বাহু অপর একটি বাহু অপেক্ষা বৃহত্তর হলে, বৃহত্তর বাহুর বিপরীত কোণ ক্ষুদ্রতর বাহুর বিপরীত কোণ অপেক্ষা বৃহত্তর হবে।
বিশেষ নির্বচন: মনে করি, ∆ABC-এ AC > AB প্রমাণ করতে হবে যে, ∠ABC > ∠ACB অঙ্কন: AC থেকে AB এর সমান করে AD অংশ কাটি এবং B, D যোগ করি।
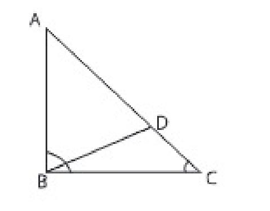
প্রমাণ:
| ধাপ | যথার্থতা |
| (১) ABD-এ AB = AD ∴ ∠ADB =∠ABD (২) BDC-এ বহিঃস্থ ∠ADB > ∠BCD ∴ ∠ABD > ∠BCD বা ∠ABD > ∠ACB (৩) ∠ABC > ∠ABD সুতরাং, ∠ABC > ∠ACB (প্রমাণিত)। | [সমদ্বিবাহু ত্রিভুজের ভূমি সংলগ্ন কোণদ্বয় সমান।] [বহিঃস্থ কোণ বিপরীত অন্তঃস্থ কোণ দুটির প্রত্যেকটি অপেক্ষা বৃহত্তর] [∠ABD কোণটি ∠ABC এর একটি অংশ] |
কোনো ত্রিভুজের একটি কোণ অপর একটি কোণ অপেক্ষা বৃহত্তর হলে, বৃহত্তর কোণের বিপরীত বাহু ক্ষুদ্রতর কোণের বিপরীত বাহু অপেক্ষা বৃহত্তর।
বিশেষ নির্বচন: মনে করি, ∆ABC' এর ∠ABC > ∠ACB প্রমাণ: |  |
| ধাপ | যথার্থতা |
| (১) যদি AC বাহু AB বাহু অপেক্ষা বৃহত্তর না হয়, তবে (i) AC = AB অথবা (ii) AC < AB হবে। | |
| (i) যদি AC = AB হয়, তবে ∠ABC = ∠ACB কিন্তু শর্তানুযায়ী ∠ABC > ∠ACB তা প্রদত্ত শর্তবিরোধী। | সমদ্বিবাহু ত্রিভুজের ভূমি সংলগ্ন কোণদ্বয় সমান। |
(ii) আবার, যদি AC < AB হয়, তবে ∠ABC ∠ACB হবে। কিন্তু তা-ও প্রদত্ত শর্তবিরোধী। ∴ AB AC এবং AC AB ∴ AC > AB (প্রমাণিত)। | [ ক্ষুদ্রতর বাহুর বিপরীত কোণ ক্ষুদ্রতর। উপপাদ্য-২ |
ত্রিভুজের যেকোনো দুই বাহুর দৈর্ঘ্যের সমষ্টির সাথে তৃতীয় বাহুর দৈর্ঘ্যের সম্পর্ক রয়েছে। সম্পর্কটি অনুধাবনের জন্য দলগতভাবে নিচের কাজটি কর।
কাজ  রুলারের সাহায্যে ত্রিভুজের বাহুগুলোর দৈর্ঘ্য মাপ এবং নিচের সারণিটি পূরণ কর। |
লক্ষ করি, যেকোনো ত্রিভুজের যেকোনো দুই বাহুর দৈর্ঘ্যের যোগফল এর তৃতীয় বাহুর দৈর্ঘ্য অপেক্ষা বেশি। আমরা আরও লক্ষ করি, যেকোনো ত্রিভুজের যেকোনো দুই বাহুর দৈর্ঘ্যের বিয়োগফল এর তৃতীয় বাহুর দৈর্ঘ্য অপেক্ষা কম।
কাজ: নিচের কোন ক্ষেত্রে ত্রিভুজ আঁকা সম্ভব- ব্যাখ্যা দাও।
১। 1 সেমি, 2 সেমি ও 3 সেমি ২। 1 সেমি, 2 সেমি ও 4 সেমি ৩। 4 সেমি, ও সেমি ও 5 সেমি |
ত্রিভুজের যেকোনো দুই বাহুর দৈর্ঘ্যের সমষ্টি এর তৃতীয় বাহুর দৈর্ঘ্য অপেক্ষা বৃহত্তর।
বিশেষ নির্বচন: ধরি ABC -এ BC বৃহত্তম বাহু। প্রমাণ করতে হবে যে (AB + AC) > BC
অঙ্কন: BA কে D পর্যন্ত বর্ধিত করি, যেন AD = AC হয়। C,D যোগ করি।
প্রমাণ:
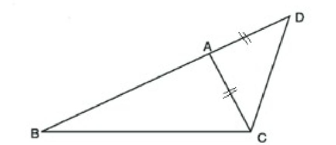
| ধাপ | যথার্থতা |
(১) ADC - এ AD = AC ∴ ∠ ACD = ∠ ADC : ∠ ACD = ∠ BDC (২) ∠ BCD > ∠ ACD ∴ ∠ BCD > ∠ BDC (৩) BCD এ ∠ BCD> ∠ BDC ∴ BD > BC (৪) কিন্তু BD = AB + AD = AB + AC ∴ (AB + AC) > BC (প্রমাণিত) | [সমদ্বিবাহু ত্রিভুজের ভূমি সংলগ্ন কোণদ্বয় সমান] [কারণ ∠ ACD , ∠ BCD এর একটি অংশ]
[ বৃহত্তর কোণের বিপরীত বাহু বৃহত্তর।] [যেহেতু AC = AD ] |

চিত্রে, CE, ∠ACD এর সমদ্বিখণ্ডক। AB || CE এবং ∠ECD = 60°
১। ∠ BAC এর মান নিচের কোনটি?
ক. 30°
খ. 45°
গ. 60°
ঘ. 120°
২। ∠ ACD এর মান নিচের কোনটি?
ক. 60°
খ. 90°
গ. 120°
ঘ. 180°
৩। ABC কোন ধরনের ত্রিভুজ?
ক. স্থূলকোণী
খ. সমদ্বিবাহু
গ. সমবাহু
ঘ. সমকোণী
8। একটি ত্রিভুজের দুটি বাহু যথাক্রমে 5 সে.মি. এবং 4 সে.মি. ত্রিভুজটির অপর বাহুটি নিচের কোনটি হতে পারে?
ক. 1 সে.মি.
খ. 4 সে.মি.
গ. 9 সে.মি.
ঘ. 10 সে.মি.
৫। সমকোণী ত্রিভুজের সূক্ষ্মকোণদ্বয়ের একটি 40 deg হলে, অপর সূক্ষ্মকোণের মান নিচের কোনটি?
ক. 40°
খ. 50°
গ. 60°
ঘ. 140°
৬। কোনো ত্রিভুজের একটি কোণ অপর দুটি কোণের সমষ্টির সমান হলে, ত্রিভুজটি কী ধরনের হবে?
ক. সমবাহু
খ. সুক্ষ্মকোণী
গ. সমকোণী
ঘ. স্থুলকোণী
৭। ∆ABC-এ AB > AC এবং ∠B ও ∠C এর সমদ্বিখণ্ডকদ্বয় পরস্পর P বিন্দুতে ছেদ করেছে। প্রমাণ কর যে, PB > PC
৮। ABC একটি সমদ্বিবাহু ত্রিভুজ এবং এর AB = AC; BC কে যেকোনো দূরত্বে D পর্যন্ত বাড়ানো হলো। প্রমাণ কর যে, AD > AB
৯। ABCD চতুর্ভুজে AB = AD, BC = CD এবং CD > AD প্রমাণ কর যে, ∠DAB > ∠BCD
১০। ∆ABC এ ∠ABC > ∠ACB. D, BC বাহুর মধ্যবিন্দু।
(ক) তথ্যের আলোকে চিত্রটি অঙ্কন কর।
(খ) দেখাও যে, AC > AB
(গ) প্রমাণ কর যে, AB+ AC > 2AD
১১। AABC-এ AB = AC এবং D, BC-এর উপর একটি বিন্দু। প্রমাণ কর যে, AB > AD
১২। ∆ABC-এ AB AC এবং D, AC-এর উপর একটি বিন্দু। প্রমাণ কর যে, BC > BD
১৩। প্রমাণ কর যে, সমকোণী ত্রিভুজের অতিভুজই বৃহত্তম বাহু।
১৪। প্রমাণ কর যে, ত্রিভুজের বৃহত্তম বাহুর বিপরীত কোণ বৃহত্তম।
১৫। চিত্রে, ∠QPM = ∠RPM এবং ∠QPR = 90°। PQ = 6 সে.মি.
ক. ∠QPM এর মান নির্ণয় কর।
খ. ∠PQM ও∠PRM এর মান কত?
গ. PR এর মান নির্ণয় কর।

প্রত্যেক ত্রিভুজের ছয়টি অংশ আছে: তিনটি বাহু এবং তিনটি কোণ। ত্রিভুজের এই ছয়টি অংশের কয়েকটি অপর একটি ত্রিভুজের অনুরূপ অংশের সমান হলে দুটি ত্রিভুজ সর্বসম হতে পারে। সুতরাং কেবল ঐ অংশগুলো দেওয়া থাকলে ত্রিভুজটির আকার নির্দিষ্ট হয় এবং ত্রিভুজটি আঁকা যায়। নিচের উপাত্তগুলো জানা থাকলে একটি নির্দিষ্ট ত্রিভুজ সহজেই আঁকা যায়:
(১) তিনটি বাহু
(২) দুটি বাহু ও এদের অন্তর্ভুক্ত কোণ
(৩) একটি বাহু ও এর সংলগ্ন দুটি কোণ
(৪) দুটি কোণ ও এর একটির বিপরীত বাহু
(৫) দুটি বাহু ও এর একটির বিপরীত কোণ
(৬) সমকোণী ত্রিভুজের অতিভুজ ও অপর একটি বাহু অথবা কোণ।
কোনো ত্রিভুজের তিনটি বাহু দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।
মনে করি, একটি ত্রিভুজের তিনটি বাহু a, b, c দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কন:
(১) যেকোনো রশ্মি BD থেকে a এর সমান করে BC কেটে নিই।
(২) B ও C বিন্দুকে কেন্দ্র করে যথাক্রমে c এবং b এর সমান ব্যাসার্ধ নিয়ে BC এর একই পাশে দুটি বৃত্তচাপ আঁকি। বৃত্তচাপ দুটি পরস্পর A বিন্দুতে ছেদ করে।
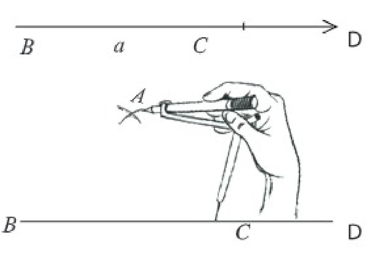
(৩) A, B এবং A, C যোগ করি। তাহলে ∆ABC-ই উদ্দিষ্ট ত্রিভুজ।
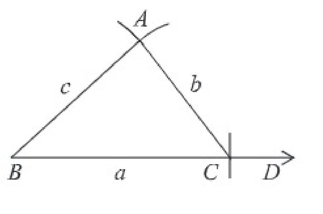
প্রমাণ: অঙ্কনানুসারে, ∆ABC এ BC = a, AC = b এবং AB = c.
∴ ∆ABC প্রদত্ত বাহুযুক্ত ত্রিভুজ।
কাজ ১। 8 সে.মি., 5 সে.মি. ও 6 সে.মি দৈর্ঘ্যের তিনটি বাহুবিশিষ্ট একটি ত্রিভুজ আঁক। ২। 12 সে.মি., 5 সে.মি. ও 6 সে.মি দৈর্ঘ্যের তিনটি বাহুবিশিষ্ট একটি ত্রিভুজ অঙ্কনের চেষ্টা কর। 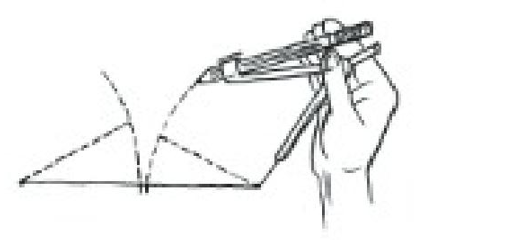 তোমার চেষ্টা সফল হয়েছে কি? |
মন্তব্য: ত্রিভুজের দুই বাহুর সমষ্টি এর তৃতীয় বাহু অপেক্ষা বৃহত্তর। তাই প্রদত্ত বাহুগুলো এমন হতে হবে যে, যেকোনো দুটির দৈর্ঘ্যের সমষ্টি তৃতীয়টির দৈর্ঘ্য অপেক্ষা বৃহত্তর হয়। তাহলেই ত্রিভুজটি আঁকা সম্ভব হবে।
কোনো ত্রিভুজের দুইটি বাহু ও এদের অন্তর্ভুক্ত কোণ দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।
মনে করি, একটি ত্রিভুজের দুইটি বাহু a ও b এবং তাদের অন্তর্ভুক্ত কোণ ∠X দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কন:
(১) যেকোনো রশ্মি BD থেকে a এর সমান করে BC নিই।
(২) BC রেখাংশর C বিন্দুতে প্রদত্ত ∠ x এর সমান ∠BCE আঁকি।
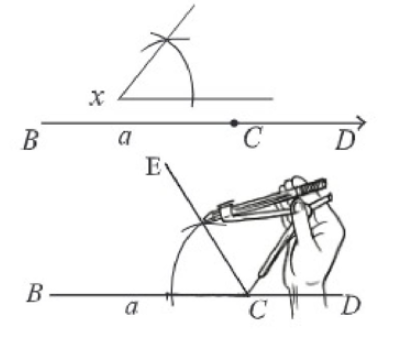
(৩) CE রেখাংশ থেকে b এর সমান করে CA নিই। A, B যোগ করি। তাহলে ABC ই উদ্দিষ্ট ত্রিভুজ।
প্রমাণ: অঙ্কন অনুসারে,
∆ABC-এ BC = a, CA = b এবং ∠ ACB = ∠ x.
∴ ∆ABC ই নির্দিষ্ট ত্রিভুজ।
কোনো ত্রিভুজের একটি বাহু ও এর সংলগ্ন দুটি কোণ দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।
মনে করি, একটি ত্রিভুজের একটি বাহু ৫ এবং এর সংলগ্ন দুটি কোণ ∠ x ও ∠ y দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

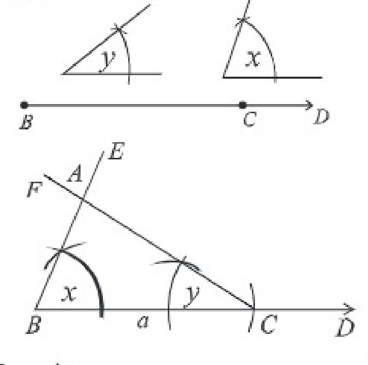
অঙ্কন:
(১) যেকোনো রশ্মি BD থেকে ৫ এর সমান করে BC নিই।
(২) BC রেখাংশের B ও C বিন্দুতে যথাক্রমে ∠ x এবং ∠y এর সমান করে ∠ CBE এবং ∠ BCF আঁকি। BE ও CF পরস্পর A বিন্দুতে ছেদ করে।
তাহলে ABC ই উদ্দিষ্ট ত্রিভুজ।
প্রমাণ: অঙ্কন অনুসারে,
ABC - 4BC = a ∠ ABC = ∠ x এবং ∠ ACB = ∠ y.
∴ ABC ই নির্দিষ্ট ত্রিভুজ।
মন্তব্য: ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণের সমান, তাই প্রদত্ত কোণ দুটি এমন হতে হবে যেন এদের সমষ্টি দুই সমকোণ অপেক্ষা ছোটো হয়। এই শর্ত পালন করা না হলে কোনো ত্রিভুজ আঁকা সম্ভব হবে না।
| কাজ ১।7 সে.মি. দৈর্ঘ্যের বাহু ও 50° ও 60° কোণবিশিষ্ট একটি ত্রিভুজ আঁক। ২।6 সে.মি. দৈর্ঘ্যের বাহু ও 140° ও 70° কোণবিশিষ্ট একটি ত্রিভুজ অঙ্কনের চেষ্টা কর। তোমার চেষ্টা সফল হয়েছে কি? কেন ব্যাখ্যা কর। |
কোনো ত্রিভুজের দুইটি কোণ এবং এদের একটির বিপরীত বাহু দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।
মনে করি, একটি ত্রিভুজের দুটি কোণ ∠A ও B এবং ∠A এর বিপরীত বাহু a দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।
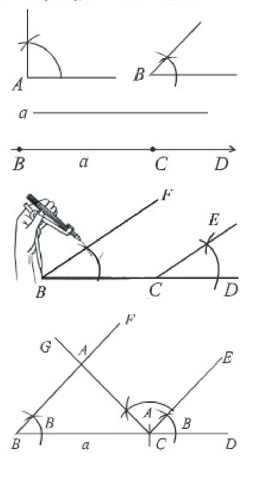
অঙ্কন:
(১) যেকোনো রশ্মি BD থেকে a এর সমান করে BC নিই।
(২) BC রেখাংশের B ও C বিন্দুতে ∠B এর সমান করে ∠CBF ও ∠DCE আঁকি।
(৩) এখন CE রেখার C বিন্দুতে ∠A এর সমান করে ∠ECG আঁকি। CG ও BF রেখা A বিন্দুতে ছেদ করে।
∴ ত্রিভুজ ABC ই উদ্দিষ্ট ত্রিভুজ।
প্রমাণ: অঙ্কনানুসারে, ∠ABC = ∠ECD. এই কোণ দুটি অনুরূপ বলে BF || CE বা BA || CE এখন BA || CE এবং AC এদের ছেদক।
∴ ∠BAC=একান্তর ∠ACE = ∠A.
এখন ∆ABC এ ∠BAC = ∠A, ∠ABC = ∠B এবং BC = a. সুতরাং, ABC ত্রিভুজটি শর্তমতে অঙ্কিত হলো।
কোনো ত্রিভুজের দুটি বাহু এবং এদের একটির বিপরীত কোণ দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।
মনে করি, একটি ত্রিভুজের দুটি বাহু a ও b এবং b বাহুর বিপরীত কোণ ∠B দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।
অঙ্কন:
(১) যেকোনো রশ্মি BD আঁকি।
(২) B বিন্দুতে প্রদত্ত ∠B এর সমান করে ∠DBE আঁকি। BE রেখা থেকে c এর সমান করে BA নিই।
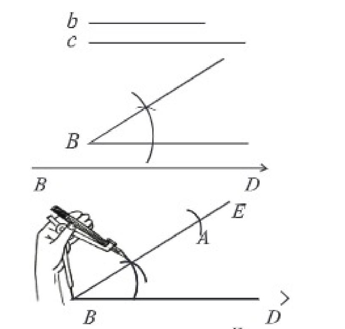
(৩) এখন এ বিন্দুকে কেন্দ্র করে ৮ এর দৈর্ঘ্যের সমান ব্যাসার্ধ নিয়ে BD রেখার উপর একটি বৃত্তচাপ আঁকি। বৃত্তচাপটি BD রেখাকে Cও C' বিন্দুতে ছেদ করে। A, C এবং A.C" যোগ করি। তাহলে ∆ABC এবং ∆ABC'-উভয় ত্রিভুজ প্রদত্ত শর্ত পূরণ করে অঙ্কিত।
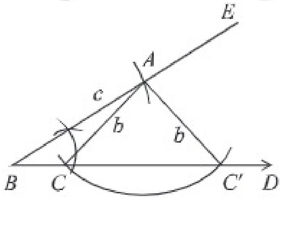
প্রমাণ: অঙ্কনানুসারে, ∆ABC এ BA = c, AC = b এবং ∠ABC = ∠B
আবার, ∆ABC" - এ BA = c, AC' = b এবং ∠ABC' = ∠B
দেখা যায়, ∆ABC এবং ∆ABC" উভয়ই প্রদত্ত শর্তসমূহ পূরণ করে।
তাহলে ∆ABC বা ∆ABC'-ই উদ্দিষ্ট ত্রিভুজ।
কোনো সমকোণী ত্রিভুজের অতিভুজ ও অপর একটি বাহু দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।
মনে করি, একটি সমকোণী ত্রিভুজের অতিভুজ a ও অপর এক বাহু b দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।
অঙ্কন:
(১) যেকোনো রশ্মি BD থেকে b এর সমান করে BC নিই।

(২) BC রেখার B বিন্দুতে BE লম্ব আঁকি।
(৩) C কে কেন্দ্র করে a এর সমান ব্যাসার্ধ নিয়ে BE রেখার উপর একটি বৃত্তচাপ আঁকি, যেন এটি BE-কে A বিন্দুতে ছেদ করে। A ও C যোগ করি। তাহলে ∆ABC-ই উদ্দিষ্ট ত্রিভুজ।

প্রমাণ: অঙ্কনানুসারে, AC = a, BC = b এবং ∠ABC = এক সমকোণ।
∴ ∆ABC-ই নির্ণেয় ত্রিভুজ।
১। কোনো ত্রিভুজের দুটি বাহু এবং এদের একটি বিপরীত কোণ দেওয়া থাকলে, সর্বাধিক কয়টি ত্রিভুজ আঁকা যাবে?
ক. 1
খ. 2
গ. 3
ঘ. 4
২। কোন ক্ষেত্রে ত্রিভুজ আঁকা সম্ভব যখন তিনটি বাহুর দৈর্ঘ্য-
ক. 1 সে.মি., 2 সে.মি. 3 সে.মি.
খ. 3 সে.মি., 4 সে.মি. 5 সে.মি.
গ. 2 সে.মি., 4 সে.মি. 6 সে.মি.
ঘ. 3 সে.মি., 4 সে.মি. 7 সে.মি.
৩। i. একটি ত্রিভুজের দুটি বাহু এবং তাদের অন্তর্ভুক্ত কোণ দেওয়া থাকলে, ত্রিভুজটি আঁকা যায়।
ii. দুটি বাহুর সমষ্টি তৃতীয় বাহু অপেক্ষা বৃহত্তর হলে, ত্রিভুজটি আঁকা যায়।
iii. কোনো ত্রিভুজের একাধিক স্থূলকোণ থাকতে পারে।
আগের পৃষ্ঠার তথ্য অনুসারে নিচের কোনটি সঠিক?
ক. i ও ii
খ. ii ও iii
গ. i ও iii
ঘ. i, ii ও iii
৪। ত্রিভুজের বাহু তিনটির দৈর্ঘ্যের সমষ্টিকে কি বলে?
(ক) ক্ষেত্রফল
(খ) আয়তন
(গ) দৈর্ঘ্য
(ঘ) পরিসীমা
৫। ত্রিভুজের অন্তঃস্থ কোণ কয়টি?
(ক) ১টি
(খ) ২টি
(গ) 3টি
(ঘ) 4টি
৬। সমবাহু ত্রিভুজের প্রত্যেকটি কোণ কত ডিগ্রি?
(ক) 30°
(খ) 45°
(গ) 60°
(ঘ) 90°
৭। একটি সমকোণী ত্রিভুজের একটি কোণ 60° হলে অপর কোনটি কত ডিগ্রি?
(ক) 30°
(খ) 60°
(গ) 90°
(ঘ) 180°
নিচের চিত্র অনুসারে ৮-৯ নম্বর প্রশ্নের উত্তর দাও:

৮। C বিন্দুতে BA রেখার সমান্তরাল রেখা আঁকতে হলে, কোন কোণের সমান কোণ আঁকতে হবে?
(ক) ∠ABC
(খ) ∠ACB
(গ) ∠BAC
(ঘ) ∠CAD
৯। ∠CAD এর সমান নিচের কোনটি?
(ক) ∠BAC + ∠ACB
(খ) ∠ABC + ∠ACB
(গ) ∠ABC+∠ACB + ∠BAC
(ঘ) ∠ABC+∠BAC
১০। একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য দেওয়া আছে। ত্রিভুজটি আঁক।
(ক) 3 সে.মি., 4 সে.মি., 6 সে.মি
(খ) 3.5 সে.মি., 4.7 সে.মি., 5.6 সে.মি
১১। একটি ত্রিভুজের দুটি বাহু ও এদের অন্তর্ভুক্ত কোণ দেওয়া আছে। ত্রিভুজটি আঁক।
(ক) 3 সে.মি., 4 সে.মি., 60°
(খ) 3.8 সে.মি., 4.7 সে.মি., 45°
১২। একটি ত্রিভুজের একটি বাহু ও এর সংলগ্ন দুটি কোণ দেওয়া আছে। ত্রিভুজটি আঁক।
(ক) 5 সে.মি., 30°, 45°
(খ) 4.5 সে.মি., 45°, 60°
১৩। একটি ত্রিভুজের দুটি কোণ ও প্রথম কোণের বিপরীত বাহু দেওয়া আছে। ত্রিভুজটি আঁক।
(ক) 120°, 30°, 5 সে.মি.
(খ) 60°, 30°, 4 সে.মি.
১৪। একটি ত্রিভুজের দুটি বাহু ও প্রথম বাহুর বিপরীত কোণ দেওয়া আছে। ত্রিভুজটি আঁক।
(ক) 5 সে.মি., 6 সে.মি., 60°
(খ) 4 সে.মি., 5 সে.মি., 30°
১৫। একটি সমকোণী ত্রিভুজের অতিভুজ ও অপর একটি বাহুর দৈর্ঘ্য দেওয়া আছে। ত্রিভুজটি আঁক।
(ক) 7 সে.মি., 4 সে.মি.
(খ) 4 সে.মি., 3 সে.মি.
১৬। একটি সমকোণী ত্রিভুজের একটি বাহু 5 সে.মি. এবং একটি সূক্ষ্মকোণ 45° দেওয়া আছে। ত্রিভুজটি আঁক।
১৭। একই সরলরেখায় অবস্থিত নয় এমন তিনটি বিন্দু A, B ও C.
ক. বিন্দু তিনটি দিয়ে একটি ত্রিভুজ আঁক।
খ. অঙ্কিত ত্রিভুজের শীর্ষবিন্দু থেকে ভূমির ওপর লম্ব আঁক।
গ. অঙ্কিত ত্রিভুজের ভূমি যে সমকোণী সমদ্বিবাহু ত্রিভুজের অতিভুজ হয়, ঐ ত্রিভুজটি আঁক।
১৮।
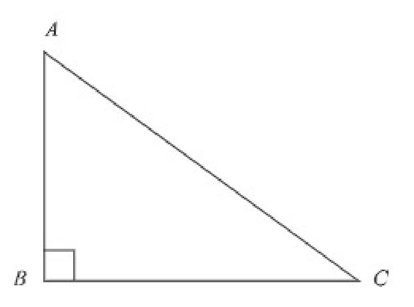
ক. সঠিক পরিমাপে ABC ত্রিভুজটি আঁক।
খ. অতিভুজের পরিমাণ সেন্টিমিটারে নির্ণয় কর এবং ∠ACB এর সমান করে একটি কোণ আঁক।
গ. একটি সমকোণী ত্রিভুজ আঁক, যার অতিভুজ চিত্রে অঙ্কিত ত্রিভুজের অতিভুজ অপেক্ষা 2 সে.মি. বড় এবং একটি কোণ, ∠ACB এর সমান হয়।
১৯। একটি ত্রিভুজের দুটি বাহু a = 3 সে.মি., b = 4 সে.মি. এবং একটি কোণ ∠B = 30°
ক. ∠B এর সমান একটি কোণ আঁক।
খ. একটি ত্রিভুজ আঁক, যার দুই বাহু a ও b এর সমান এবং অন্তর্ভুক্ত কোণ ∠B এর সমান হয়।
গ. এমন একটি ত্রিভুজ আঁক, যার একটি বাহু b এবং ∠B এর বিপরীত বাহু 2a হয়।
২০। একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য = 4 সে.মি., b = 5 সে.মি., c= 6 সে.মি.
(ক) একটি সমবাহু ত্রিভুজ অঙ্কন কর।
(খ) ত্রিভুজটি অঙ্কন কর। (অঙ্কনের চিহ্ন ও বিবরণ আবশ্যক)
(গ) এমন একটি সমকোণী ত্রিভুজ অঙ্কন কর যেন সমকোণ সংলগ্ন বাহুদ্বয় a ও b এর সমান হয়।
(অঙ্কনের চিহ্ন ও বিবরণ আবশ্যক)
২১। AB ও CD দুটি সমান্তরাল সরলরেখা PQ রেখাটি AB ও CD রেখাকে যথাক্রমে E ও F বিন্দুতে ছেদ করেছে।
(ক) বর্ণনা অনুযায়ী চিত্র অঙ্কন কর।
(খ) দেখাও যে, ∠AEP = ∠CFE
(গ) দেখাও যে, ∠AEF + ∠CFE = ২ সমকোণ
common.read_more